The impact of the Fiscal Compact on a ‘Good’ Country

Much of the early part of the referendum campaign has been focussed on the possible implications of the Treaty on Stability, Coordination and Governance in post-2015 Ireland when we are due to leave the Excessive Deficit Procedure.  In reality the Treaty will change very little as we are already bound by the rules in the Stability and Growth Pact, and even in the absence of rules the scope for discretionary fiscal policy in Ireland is going to be extremely limited for the medium term given the precarious state of the public finances.

It may be useful to consider the impact of the rules in the fiscal compact in a country that is currently in adherence of both the 3% of GDP deficit limit and the 60% of GDP debt limit from the Maastricht Treaty.  What will the impact of the rules be on such a country?  At present examples of such countries are scarce as 14 of the eurozone 17 are in an Excessive Deficit Procedure due to breaching the 3% of GDP deficit limit.  One example we can use is Finland.

According to the recent Maastricht Returns, Finland finished 2011 with a debt equal to 48.6% of its GDP and had a budget deficit equal to 0.5% of GDP.  Finnish GDP was around €191.5 billion in 2011.  According the Finland’s Apil 2012 Stability Programme Update, Finland had a structural budget balance of +0.9% in 2011 and an output gap of –3.5% of GDP.  Finland has a medium term budgetary objective (MTO) of +0.5% of GDP and was the only eurozone country to meet its MTO in 2011.

So let’s create a hypothetical country (but based loosely around the example of Finland).

• Initial general government debt: 50% of GDP
• Medium term budgetary objective: –0.5% of GDP
• Output gap: –4% of GDP to +2% of GDP over the cycle
• Elasticity of budget balance to output gap: 0.5
• Average nominal GDP growth: 4% per annum

To simplify things we will assume that the country always hits the MTO and that the output gap improves from –4% of GDP by one percentage point a year up to +2% of GDP and declines in the same fashion to –4% of GDP and so on.  We will let nominal GDP growth average 4% per annum (say 2% inflation plus 2% real growth) and we will artificially assume that it follows a pattern of the output gap +5% so that it ranges from 1% to 7% over the cycle. 

As this country has a debt ratio below the 60% reference value we do not need to consider the impact of the ‘1/20th’ debt brake rule as it does not apply.  Thus we can focus on the structural deficit rule which was introduced in Council Regulation 1055/2005 in June 2005.

What happens to the debt and deficits in the hypothetical country described above if it adheres to the fiscal rules?  As the example is highly stylized it is relatively easy to see what will happen to the overall deficits.

Allowable Deficit = Structural Deficit + (Elasticity x Output Gap)

So when the output gap is -4% of GDP, –2% of GDP, 0% of GDP and 2% of GDP it can be seen that:

• At –4% Output Gap: Deficit = –0.5% + (0.5 x -4.0) = -2.5%
• At –2% Output Gap: Deficit = –0.5%  + (0.5 x 2.0) = -1.5%
• At 0% Output Gap:  Deficit = –0.5% + (0.5 x 0.0) = –0.5%
• At +2% Output Gap: Deficit = –0.5% + (0.5 x 2.0) = +0.5%

Over the course of the business cycle the overall deficit ranges between –2.5% of GDP at the trough to +0.5% at the peak.  The deficit keeps within the overall 3% of GDP limit and while it is counter-cyclical one question is whether it is counter-cyclical enough?

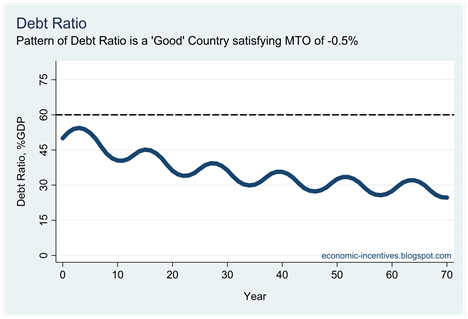
Here is what happens to the debt ratio over a 70 years period.

Again it can be seen that the pattern is cyclical, and if the economic cycle was included, it would be seen that it is counter-cyclical.  The debt ratio falls in good times, which here are when nominal growth is greater than 4% per annum, and rises when the nominal growth rate falls below this.  If inflation was 2% the inversion point would be real growth of 2% per annum.  Again there is the question of whether it is counter-cyclical enough. 

With the debt ratio there is the added question of whether it is “too low”.  The debt ratio starts off at 50% of GDP but as can be seen there is a downtrend as well as a cyclical trend.  With the assumptions here, there are overall deficits that average 1% of GDP and average nominal growth of 4% per annum so the debt will converge on a level equal to 25% of GDP.  That has happened at the end of the time period show above.  

This is well below the 60% threshold set in the Maastricht criteria and this value is never threatened.

For those concerned about debt repayments can note that the debt ratio falls in 41 of the years shown above, but that the amount of debt only falls in 6 of those (when there is a budget surplus).  There are 35 years where the debt ratio falls, while the level of debt doesn’t.

This is a highly stylized example and reality does not fit the straight line assumptions used here but it can be used as a gauge of what the rules are supposed to imply in theory.

Countries are not always going to exactly meet their MTO and some slippage in bad times is likely.  This would keep the debt ratio higher than is shown here.  If the average deficit was 1.6% of GDP over the cycle (rather than 1%) then the debt ratio here would converge on 40% of GDP.

For a good country it can be shown that deficits will vary with the cycle (but maybe not by enough) and that the debt will fall to sustainable levels (but maybe by too much).  Whatever about their application now (and it is actually the Excessive Deficit Procedure that is driving fiscal policy now) the rules themselves do seem like reasonable efforts at prudent fiscal management that offer some room for counter-cyclicality though this is based entirely on automatic stabilisers rather than discretionary measures.

Tweet